Астрофизикам не удается снизить «хаббловское напряжение»

Постоянная Хаббла определяет скорость расширения современной Вселенной и потому представляет огромный интерес для астрофизики и космологии. Ее численные значения многократно оценивались разными способами без малого сто лет и в начале нашего века считались установленными достаточно надежно и в довольно узком интервале.

Однако в прошлом десятилетии стали публиковаться другие значения постоянной Хаббла, которые оказались приблизительно на 10% меньше предшествующих. Это расхождение, получившее название Hubble tension («хаббловское напряжение»), до сих пор так и не удалось устранить. Для его объяснения выдвинуто великое множество гипотез, однако к решению проблемы они не привели. Недавно был опубликован ряд статей на эту тему, основанных на последних данных, полученных, в том числе, и на космическом телескопе имени Джеймса Уэбба. Описанные результаты, из-за того, что они более точные, даже усугубляют проблему.

Немного истории

Начнем с самого начала — ab ovo. В конце 1920-х годов американский астроном Эдвин Хаббл и его ассистент Милтон Хьюмасон занялись уточнением расстояний до десятков космических туманностей за пределами Млечного Пути, которые лишь несколькими годами ранее стали считать самостоятельными галактиками. Эти звездные скопления двигались прочь от Солнца с радиальными скоростями, которые были измерены по величине красного смещения их спектров на основе эффекта Доплера — Физо. Хотя дистанции до большинства таких галактик удалось определить с большой погрешностью, Хаббл все же пришел к заключению, что между ними и скоростями скорее всего существует универсальная линейная зависимость.

Об этом он написал в статье, опубликованной в начале 1929 года (E. Hubble, 1929. A relation between distance and radial velocity among extra-galactic nebulae). В 1931 году Хаббл и Хьюмасон подтвердили свой вывод на основании результатов наблюдений других галактик, некоторые из которых отдалены от Солнца более, чем на 100 миллионов световых лет (E. Hubble, M. Humason, 1931. The Velocity-Distance Relation among Extra-Galactic Nebulae). В этой работе утверждается, что радиальные скорости туманностей возрастают приблизительно на 558 км/сек с каждым увеличением расстояния до них на миллион парсек. При этом особо подчеркивается, что имеются в виду видимые скорости удаления туманностей от Земли, как они определяются из их красного смещения на основе эффекта Доплера.

Собранная Хабблом и Хьюмасоном информация легла в основу прославленной формулы \(v=H_0d\), известной как закон Хаббла (точнее, здесь приведена исторически первая форма математической записи этого закона, о чем подробней будет сказано ниже). Здесь \(v\) — радиальная скорость галактики по отношению к Земле, \(d\) — расстояние, \(H_0\) — коэффициент пропорциональности, чья размерность, как легко видеть, обратна размерности времени. Сам Хаббл и еще многие астрономы долгое время отказывались от предположений о физическом смысле этого коэффициента. Тем более интересно, что молодой бельгийский космолог Жорж Леметр еще в 1927 году показал, что общая теория относительности позволяет интерпретировать разлет галактик как свидетельство расширения Вселенной (G. Lemaître, 1927. Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques). Более того, он математически вывел полный аналог будущей хаббловской формулы и, располагая известными к тому времени данными о скоростях ряда галактик и расстояниях до них, получил примерно такое же численное значение коэффициента пропорциональности между дистанциями и скоростями, что и Хаббл. Однако его статья была напечатана по-французски в малоизвестном бельгийском журнале и поначалу осталась незамеченной. Большинству астрономов (почти наверняка, и самому Хабблу) она стала известна лишь в 1931 году после публикации ее английского перевода.

Разумеется, история открытия и, если воспользоваться известным выражением Менделеева, укрепления закона Хаббла гораздо богаче этой схемы. Она подробно описана в биографиях Хаббла и Леметра, вошедших в мою книгу о великих творцах современной науки о физике космоса (А. Е. Левин, 2022. Астрофизика в лицах: с. 139–166 и 167–180). Мы же теперь можем перейти от былых времен к двадцать первому веку.

Вселенная и закон Хаббла

Бесчисленные астрономические наблюдения давно показали, что мы живем в однородной и изотропной Вселенной, которая практически с самого рождения претерпевает перманентное расширение. Это означает, что физические расстояния между гравитационно независимыми галактиками и скоплениями галактик постоянно возрастают, однако крупномасштабная геометрия пространства Большого Космоса неизменно сохраняет однородность и изотропию. Выражаясь менее формально, в этой геометрии нет ни выделенных мест, ни выделенных направлений — так сказать, имеет место идеальная вселенская демократия.

Как показывает математический анализ, однородное и изотропное трехмерное пространство может существовать лишь в трех версиях — сферической, плоской (это наше родное пространство Евклида) и гиперболической. Всем им соответствует метрика Леметра — Фридмана — Робертсона — Уокера, которая тоже задается в трех вариантах. Формально различия между ними задаются параметром, определяющим знак (но не абсолютную величину!) кривизны пространства: для сферической геометрии она положительна, для евклидовой — нулевая, и для гиперболической — отрицательна. Как показывают многочисленные астрономические наблюдения, реальная пространственная кривизна сегодняшней Вселенной в принципе может быть отлична от нуля, однако же очень к нему близка. Это можно выразить и иначе: радиус кривизны пространства Вселенной может быть конечен, но в любом случае он намного превышает линейные размеры той ее части, которая доступна нашим наблюдениям.

Для описания расширения пространства в метрику вводится так называемый масштабный фактор \(a(t)\), который увеличивается со временем (см. задачу Очень темные дела). Принято считать, что сегодня он равен единице, а при приближении к началу Вселенной уменьшается и в конечном счете стремится к нулю.

А теперь самое главное. Растяжение пространства увеличивает длины волн всех электромагнитных излучений, которые распространяются в космосе между гравитационно не связанными объектами. Более того, это увеличение пропорционально росту масштабного фактора. Отсюда следует, что длина волны светового кванта, испущенного где-то в космосе в прошлую эпоху в момент времени \(t\) и теперь достигшего нашей планеты, увеличится по сравнению с первоначальным значением в отношении \(\frac1{a(t)}\) (поскольку \(a(t)\) меньше единицы, эта дробь превышает единицу). Этот феномен называется космологическим красным смещением. Его можно записать с помощью простой формулы:

\[\frac{\lambda_0}{\lambda(t)}=\frac1{a(t)},\]

где \(\lambda(t)\) — длина волны фотона в момент испускания, а \(\lambda_0\) — его же длина волны в момент земного наблюдения (напомню, что здесь единица — это конвенциональное значение масштабного фактора в нашу эпоху).

Пойдем дальше. Отношение прироста длины волны к исходному значению \(\frac{\lambda_0-\lambda(t)}{\lambda(t)}\), принято обозначать буквой \(z\). Это безразмерная функция времени, которая одновременно равна относительному изменению масштабного фактора \(\frac{1-a(t)}{a(t)}\). Так что \(z(t)\) — это и есть численная мера космологического красного смещения. Из ее определения следует, что чем дальше от Земли источник фотонов, тем больше их красное смещение.

И еще одно определение — последнее и самое важное. В космологии вводится параметр \(H(t)\), равный отношению производной масштабного фактора по времени к его величине в тот же момент. Легко видеть, что размерность этого параметра обратна размерности времени (например, это 1/сек, если измерять время в секундах). Его называют параметром Хаббла, а его современное значение H₀ — постоянной Хаббла.

Довольно элементарные соображения позволяют показать, что если момент момент испускания фотона \(t\) достаточно близок к «нашему» космическому времени \(t_0\) (или, что то же самое, если источник света в космологических масштабах не слишком удален от Земли), имеет место простое, но замечательное соотношение \(z(t) =H_0(t_0-t)\). Если умножить обе его части на скорость света \(c\), то справа получим постоянную Хаббла, умноженную на расстояние до источника излучения \(d = c(t_0-t)\), вычисленное с точностью до малых поправок. Так что окончательно имеем \(cz=H_0d\). Это и есть закон Хаббла, как он формулируется в астрономии и космологии. Он переходит в классическую формулу Хаббла \(v=H_0d\), если вспомнить, что, согласно теории эффекта Доплера — Физо, величина красного смещения при взаимном удалении источника и приемника света дается формулой \(z=\frac vc\), которая справедлива, если скорость удаления \(v\) много меньше световой.

Если выбрать, как это обычно и делается, систему единиц, в которой скорость света \(c=1\), закон Хаббла приобретает совсем уж простой вид \(z=H_0d\). При ее использовании в такой записи надо только помнить, что размерности пространственной длины и времени в этой системе совпадают. Практически она применима, если величина красного смещения не превышает одной десятой.

Как уже говорилось, значение постоянной Хаббла можно выражать в обратных секундах. Однако реально для него используют запись, восходящую к исходной хаббловской формуле \(v=H_0d\). Поскольку слева там стоит скорость разлета галактик, выраженная в километрах в секунду, удобно «врезать» эту же меру и в определение хаббловской константы, придав ей размерность скорость/расстояние. Конкретно, ее численные значения определяют в километрах в секунду на мегапарсек, выражая межгалактические дистанции \(d\) опять-таки в мегапарсеках. Именно так и поступил Хаббл. Правда, в его совместной статье с Хьюмасоном от 1931 года численная величина \(H_0\) оценивалась в 558 (км/сек)/Мпк, что уже тогда выглядело сильно завышенным. Первым астрономом, получившим близкое к современному значение хаббловской константы, был блестящий мастер прецизионных телескопических наблюдений американец Аллан Сэндидж, который в 1958 году, уже после кончины Хаббла, определил величину \(H_0\) в 75 (км/сек)/Мпк. С тех пор она многократно корректировалась и продолжет корректироваться. Результаты этих корректировок и привели к возникновению так называемого Hubble tension («хаббловского напряжения»).

Еще одно техническое уточнение состоит в том, что хаббловская интерпретация космологического красного смещения в контексте эффекта Доплера исторически вполне объяснима, но с современной точки зрения не всегда верна и в любом случае не необходима. Поэтому для пущей ясности повторю, что корректная запись закона Хаббла дается формулой \(cz=H_0d\) (или \(z=H_0d\), еcли считать, что \(c=1\)).

Можно спросить, почему задача возможно более точного определения величины \(H_0\) настолько релевантна для наук о космосе. Все дело в том, что космологические модели, описывающие эволюцию Вселенной, прямо или косвенно опираются на современное значение параметра Хаббла \(H_0\). В частности, его обратная величина \(\frac{1}{H_0}\) по порядку величины равна возрасту Вселенной, а произведение \(\frac{1}{H_0}\) на скорость света характеризует масштаб ее видимой области. Поэтому для астрономии и космологии выяснение точного значения \(H_0\) не менее важно, чем, скажем, для физики частиц измерение заряда и массы электрона.

В заключение этого раздела хочу сильно облегчить жизнь и себе, и читателям. В дальнейшем речь пойдет о разных способах и результатах оценки постоянной Хаббла, что надо было бы подкрепить многочисленными ссылками. Это загромоздило бы мой скромный труд и вряд ли бы представило интерес для аудитории «Элементов». Поэтому сошлюсь только на один источник библиографической информации, зато чрезвычайно репрезентативный. В конце прошлого года в электронном архиве препринтов был выложен очень полный обзор всего круга проблем, связанных с Hubble tension — L. Verde et al., A Tale of Many H₀. Помимо демонстрации литературной эрудиции авторов, озаглавивших свою работу с намеком на известный роман Чарльза Диккенса, этот обзор содержит огромный массив библиографических данных. Полагаю, что его будет вполне достаточно. Ссылки на публикации нынешнего года я предложу в заключительном разделе.

Оптические методы оценки \(H_0\)

В принципе, путь к определению постоянной Хаббла с помощью фотометров, установленных на оптических (в том числе, и инфракрасных) телескопах вполне элементарен. Надо найти во Вселенной побольше не слишком удаленных объектов с надежно установлеными расстояниями от Солнца, измерить их красные смещения спектрографами, и вычислить \(H_0\) простой арифметикой. Дистанции до самых близких объектов можно вычислять посредством измерения их годичных параллаксов, то есть, чисто астрометрическими способами. Для дистанций побольше применяются наблюдения космических тел с известными светимостями, так называемых стандартных свечей. В этом качестве удобно использовать переменные звезды (например, цефеиды) с установленными соотношениями между периодами и светимостями. В частности, именно с цефеидами работал Эдвин Хаббл. Как отмечено в цитированном обзоре, многочисленные наблюдения цефеид позволили придти к заключению, что \(H_0\) с хорошей точностью можно считать равной 73,1±2,5 (км/сек)/Мпк.

Другая часто используемая разновидность стандартных свечей — это сверхновые типа Ia. Они имеют схожую пиковую светимость, примерно в четыре миллиарда раз превышающую солнечную. Это постоянство отнюдь не абсолютно, отклонения от среднего уровня достигают 20–30%, но их учет — решаемая проблема.

Конечно, все просто только на словах. Как и в случае цефеид, калибровка сверхновых сопряжена с серьезными техническими трудностями (необходимо принимать в расчет космическую пыль и много чего еще). Здесь уместно вспомнить, что открытие в самом конце прошлого столетия ускоренного расширения Вселенной опиралось как раз на наблюдение сверхновых из этого семейства и потому было бы невозможным без надлежащего учета всех этих факторов. В ходе этих наблюдений был накоплен большой опыт в «работе» со сверхновыми типа Ia, который пригодился и в их использовании для оценки величины \(H_0\). Согласно авторам обзора, на сегодня самое точное значение постоянной Хаббла, полученное с помощью наблюдений сверхновых, равно 73,29±1,15 (км/сек)/Мпк. Как видим, оно очень близко к цефеидной оценке.

Еще одна возможность состоит в наблюдении звезд, лежащих на ветви красных гигантов. Чтобы понять, что это такое, обратимся к судьбе нашего Солнца. Через 5,4 миллиарда лет в его ядре выгорит весь водород, дав начало гелию. Когда это произойдет, Солнце потеряет гидростатическую стабильность и начнет расширяться, превращаясь в красный гигант. Этот процесс займет около двух миллиардов лет и приведет к тому, что солнечный радиус вырастет где-то в 250 раз, светимость Солнца увеличится в 2700 раз, а температура его атмосферы упадет до 2650 К. В это время многократно возрастет интенсивность солнечного ветра, что приведет к потере тридцати процентов солнечной массы.

На этом изменения не закончатся. Солнечное ядро будет постепенно сжиматься, увеличивая свою температуру. Приблизительно через 12 миллиардов лет она дойдет до ста миллионов кельвинов, и в ядре начнется взрывообразное термоядерное горение гелия (так называемая гелиевая вспышка) приводящее к синтезу углерода и кислорода. На этой стадии Солнце претерпит двадцатикратное сжатие, а температура его поверхности подрастет до 4770 К, так что наше постаревшее светило из красного сделается оранжевым.

Фаза гелиевого горения будет не слишком продолжительной — всего лишь порядка сотни миллионов лет. В это время вокруг ядра будет дожигаться водород, причем зона его сгорания сдвинется по направлению к солнечной поверхности. Когда запасы гелия иссякнут, Солнце опять потеряет стабильность, и его внешние слои расширятся практически до прежнего максимума. Температура Солнца опять упадет, на этот раз до 3100 кельвинов, и оно очутится на так называемой асимптотической ветви красных гигантов. Наконец, примерно через 30 миллионов лет Солнце выбросит свои оболочки в окружающее пространство, дав начало так называемой планетарной туманности, а его ядро превратится в медленно остывающий углеродно-кислородный белый карлик.

Я опустил ряд деталей этого сценария, но главное не в них. Чтобы в ядре загорелся гелий, давление там должно превысить критический порог, что происходит при массе ядра порядка половины нынешней солнечной массы. Поэтому светимость и поверхностная температура (следовательно, и цвет) у звезд в этой фазе более или менее одинаковы. Поскольку по ее достижении звезды вновь охлаждаются и их светимость резко падает, ветвь, которую они населяют на диаграмме «температура-светимость», обрывается. А перед началом гелиевого горения все звезды с массой не свыше 1,8 солнечной имеют схожие светимости, которые лежат в диапазоне 2000–3000 светимостей Солнца. Область на диаграммах Герцшпрунга — Расселла, где наблюдается этот обрыв, называется вершиной ветви красных гигантов (the tip of the red giant branch, TRGB).

Первое предложение использовать TRGB в качестве стандартных свечей было выдвинуто еще в конце прошлого века. Сейчас этот метод используют для надежной калибровки космических дистанций вплоть до дистанций порядка 20 Мпк. Этот масштаб меньше по сравнению с масштабами цефеидной калибровки, но вполне приемлем. С другой стороны, число галактик, где наблюдаются вершины ветви красных гигантов, где-то в пять раз превышает число галактик с выявленными цефеидами (пятьсот против ста). Кроме того, использование наблюдений на телескопе имени Джеймса Уэбба (JWST) дает надежду довести масштаб дистанционных измерений до 50 Мпк.

Результаты различных коллабораций, наблюдающих вершины ветвей красных гигантов, пока не свелись к единой оценке \(H_0\). В обзоре приведены три значения: 69,8±0,8 (км/сек)/Мпк, 71,5±1,8 (км/сек)/Мпк и 73,22±2,06 (км/сек)/Мпк.

Я описал основные методы оптической калибровки расстояний в относительной близости от Солнца и определения на их основе величины постоянной Хаббла. Не хочу загромождать статью перечислением других способов, хотя они тоже имеют место. В целом, разброс полученных таких образом величин составляет 3–5 (км/сек)/Мпк. Можно предположить, что по мере усовершенствования измерительных технологий и обработки результатов (в частности, с помощью искусственного интеллекта, который уже начал применяться) этот разброс удастся ужать. Пожалуй, больше здесь пока ничего и не скажешь.

Волны космических звуков

Оптические наблюдения с прямыми измерениями красного смещения дали огромный массив информации, но отнюдь не стали единственным средством оценки постоянной Хаббла. В нашем столетии появились и стали быстро развиваться другие способы решения той же задачи, использующие не оптические, а радиотехнические методы наблюдений. Их применение привело к тому, что набор вычисленных значений этой константы сделался бимодальным — иначе говоря, они стали группироваться около двух показателей, отделенных друг от друга весьма значительной щелью. Именно так и возникла хаббловская контраверза, она же Hubble tension.

Новые значения постоянной Хаббла были получены благодаря наблюдениям реликтового излучения, рожденного приблизительно через 380 тысяч лет после Большого взрыва. На этой стадии эволюции мироздания завершился так называемый процесс рекомбинации, который привел к тому, что в космическом пространстве стали почти свободно распространяться световые кванты, которые ранее были «сцеплены» с электронами в составе первичной плазмы. Это стало возможным из-за того, что благодаря постепенному остыванию вещества Вселенной практически все свободные электроны соединились с ядрами водорода, гелия и лития и тем положили начало нейтральным атомам.

Реликтовое излучение служит важнейшим источником информации не только о состоянии тогдашней Вселенной, но и об ее ранней и даже очень ранней истории. О том, как его открыли и какую информацию оно несет, можно прочитать в моей книге Белые карлики. Будущее Вселенной (с. 217–261).

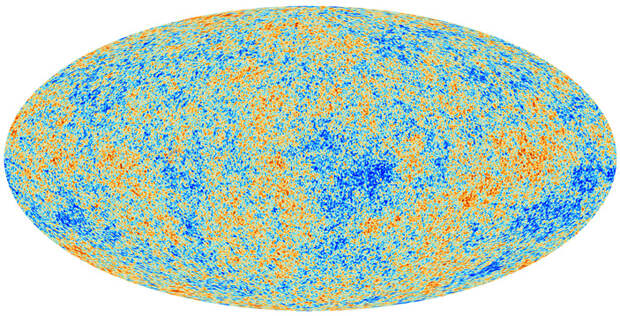
Очень кратко, дело здесь в следующем. Сегодня спектр реликтового излучения с большой точностью совпадает со спектром излучения абсолютно черного тела, имеющего температуру 2,725 К. С большой точностью — но не полностью. Температура и поляризация реликтовых фотонов очень незначительно варьируют в зависимости от направлений, с которых они приходят к Земле. Это означает, что реликтовое излучение слабо анизотропно как по температуре, так и по поляризации. Тонкий анализ спектральных характеристик этой анизотропии позволяет получить информацию о величине основных параметров, определяющих эволюцию Вселенной, — например, о плотности барионной и темной материи. К числу этих параметров относится и постоянная Хаббла \(H_0\).

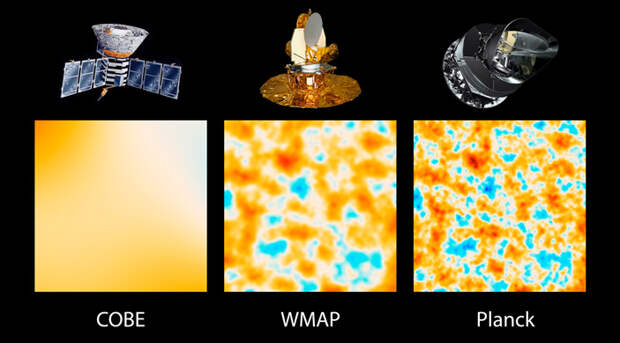
Теперь займемся происхождением упомянутой бимодальности. Исторически оно совпадает с самым началом нашего столетия. 30 июня 2001 года НАСА отправило в космос зонд Explorer 80, через два года переименованный в WMAP (Wilkinson Microwave Anisotropy Probe). Его аппаратура позволила регистрировать температурные флуктуации микроволнового реликтового излучения (МРИ) с угловым разрешением менее трех десятых градуса. Тогда уже было известно, что спектр этого излучения почти полностью совпадает со спектром абсолютно черного тела, нагретого до 2,725 К, а колебания его температуры при «крупнозернистых» измерениях с угловым разрешением в 10 градусов не превышают 0,000036 К. Однако на «мелкозернистой» шкале зонда WMAP амплитуды таких флуктуаций были в шесть раз больше (около 0,0002 К). Реликтовое излучение оказалось пятнистым, тесно испещренным чуть более и чуть менее нагретыми участками.

Флуктуации реликтового излучения порождены колебаниями плотности электронно-фотонного газа, который некогда заполнял космическое пространство. Она упала почти до нуля приблизительно через 380 тысяч лет после Большого взрыва, когда завершился процесс рекомбинации, о котором говорилось выше. Пока этого не произошло, в электронно-фотонном газе распространялись звуковые волны, на которые влияли гравитационные поля частиц темной материи. Эти волны, или, как говорят астрофизики, барионные акустические осцилляции, наложили отпечаток на спектр реликтового излучения. Расшифровка этого спектра при помощи теоретического аппарата космологии и магнитной гидродинамики дала возможность по-новому оценить постоянную Хаббла.

Сначала результаты аппаратуры обсерватории WMAP, полученные на основе первых трех, пяти и семи лет ее работы, давали не слишком беспокоящие значения постоянной Хаббла в промежутке 70–71 (км/сек)/Мпк, которые лишь немного уступали тогдашнему консенсусному показателю 73–74 (км/сек)/Мпк. Однако в 2012 году данные с той же обсерватории позволили вычислить новое значение хаббловской постоянной, которое сдвинулось к 69 (км/сек)/Мпк. Это уже вызывало беспокойство, которое, правда, тогда отнюдь не всеми было осознано.

Как оказалось, это было только начало. В 2013 году Европейского космическое агентство опубликовало детальный отчет о результатах работы космической обсерватории «Планк», запущенной к второй точке Лагранжа 14 мая 2009 года. Подобно WMAP, она занималась детальными промерами интенсивности и поляризации МРИ, причем по всей небесной сфере и на девяти частотных полосах в диапазоне от 30 до 857 гигагерц. Обработка полученных результатов позволила дать еще более низкую оценку величины \(H_0\): 67,80±0,77 (км/сек)/Мпк. Примерно такими же оказались и следующие результаты, опубликованные в 2015 и 2018 годах. Весь набор результатов «Планка», если не считать явно аномальных, укладывается в промежуток 64–70 (км/сек)/Мпк, причем наиболее убедительные величины лежат в его центре. Поскольку, как уже говорилось, до тех пор оптические наблюдения различных космических объектов неизменно показывали, что \(H_0\) принадлежит диапазону 73–74 (км/сек)/Мпк (или, по крайней мере, не слишком из него выходит), у космологов и астрофизиков возникли вполне реальные причины для беспокойства.

Последние результаты

К сказанному осталось добавить немного. В 2024 году были обнародованы итоги ряда новейших наблюдений, которые, пожалуй, только усложнили проблему Hubble tension. В январе группа под руководством одного из первооткрывателей ускоренного расширения Вселенной Адама Рисса с очень высокой достоверностью подтвердила эффективность методов определения постоянной Хаббла с помощью наблюдения цефеид и сверхновых звезд, используя информацию, полученную аппаратурой Космического телескопа имени Джеймса Уэбба. Другая группа с его участием в самом конце февраля обнародовала информацию о численном значении постоянной Хаббла, полученную с помощью фотометрических наблюдений вершины асимптотической ветви красных гигантов (этот метод имеет много общего с TRGB, но я позволю себе воздержаться от подробностей). Их оценки лежат в диапазоне 71–78 (км/сек)/Мпк с фидуциальным значением 74,7±(системные и статистические поправки) (км/сек)/Мпк.

В апреле результаты «Планка» практически повторила международная коллаборация DESI (Dark Energy Spectroscopic Instrument). Ее значение \(H_0=67{,}53\pm0{,}38\) (км/сек)/Мпк получено на основе выявления барионных акустических осцилляций посредством оптической спектроскопии света далеких галактик. Конечно, наблюдаются не сами эти осцилляции, а их следы, только на этот раз «впечатанные» не в анизотропию реликтового излучения, а в крупномасштабные трехмерные структуры космической материи — например, скопления галактик (популярное изложение этого метода можно найти в статье L. Linke, 2024. Euclid — The Dark Universe detective).

В принципе, это сообщение не отличается абсолютной новизной. Четырьмя годами ранее близкие результаты уже были извлечены из данных, полученных в ходе предшествующего трехмерного картирования космического пространства в рамках Слоановского цифрового обзора космоса (Sloan Digital Space Survey, SDSS). Летом 2020 года одна из коллабораций-участников этого проекта оценила постоянную Хаббла в 68 (км/сек)/Мпк. С другой стороны, надо отметить, что в литературе к результатам команды DESI уже появилось немало вопросов, и нельзя исключить, что они будут скорректированы или даже опровергнуты. Как бы то ни было, бимодальность значений постоянной Хаббла никуда не делась, и как от нее избавиться, пока не известно.

Очень короткое заключение

Однако кое-какие предположения сделать можно. Легко заметить, что в основе бимодальности лежит тот простой факт, что численные значения постоянной Хаббла оцениваются на основе двух принципиально различных подходов. Оценки верхней моды выводятся на основе регистрации фотонных потоков, рожденных относительно недавно и не так далеко от Земли — конечно, по космологическим масштабам. Фигурально выражаясь, они несут информацию о событиях, которые на космологической шкале времен и дистанций имеют место hic et nunc, здесь и сейчас. А вот реликтовое излучение дошло к нам от эпохи рекомбинации, имевшей место, округленно, всего лишь через 400 тысяч лет после Большого взрыва. Разница бросается в глаза.

Я попросил прокомментировать проблему Hubble tension одного из ведущих российских специалистов по космологии члена-корреспондента РАН Дмитрия Сергеевича Горбунова. Он сказал, что не видит другого объяснения кроме гипотезы, что либо перед началом рекомбинации, либо незадолго до нашего времени случилось что-то такое, что сделало невозможной однозначную оценку постоянной Хаббла. Что именно — тайна сия велика есть. Если так, остается надеяться, что когда-нибудь ее удастся разгадать. А надежды питают не только юношей, но также астрономов и космологов любых возрастов.

Источники:
1) A. Riess et al., 2024. JWST Observations Reject Unrecognized Crowding of Cepheid Photometry as an Explanation for the Hubble Tension at 8 sigma Confidence // электронный препринт arXiv:2401.04773 [astro-ph.CO].
2) S. Li et al., 2024. Reconnaissance with JWST of the J-region Asymptotic Giant Branch in Distance Ladder Galaxies: From Irregular Luminosity Functions to Approximation of the Hubble Constant // электронный препринт arXiv:2401.04777 [astro-ph.CO].
3) DESI Collaboration. DESI 2024 VI: Cosmological Constraints from the Measurements of Baryon Acoustic Oscillations // электронный препринт arXiv:2404.03002 [astro-ph.CO].

Алексей Левин

Adblock test (Why?)